2025.02.01


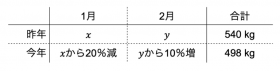
今年の1月と2月の二酸化炭素の排出量をそのまま文字に置き換えるのではなく、 昨年のそれぞれの二酸化炭素の排出量をxとyとした。
問題文を読む中で、昨年の二酸化炭素の排出量を計算できれば、 聞かれている今年の二酸化炭素の排出量も算出することができる。
また、昨年の二酸化炭素の排出量をそれぞれ文字に仮定することで、 今年の二酸化炭素の排出量もその文字を使って表すことができることも読み取れるため、 求められている数値以外のものをxとyにすることがポイント。
問題文の内容を整理すると、下記の表になります。
連立方程式の文章題では、最初に何を文字に置くかを明記する。
その際に、しっかりと単位も書く。
今回の問題のように、文字に仮定した数と答えが違うので、計算結果をもとに、しっかりと答えまで計算すること。