城南コベッツ東大宮教室

■変数が負の値をとるときの比例の関係

（例）東西にのびる一直線の道路を東へ向かって時速６㎞で歩いている人が、A地点を通過してから χ 時間後にA地点からｙ㎞のところにいるとする。東の方向を正の方向とするとき

（１）χとｙの関係を式に表すと（道のり）＝（速さ）×（時間）なので、

　　ｙ＝６χ

（２）χ＝－３（－３時間後）のときのｙを求めるとＡ地点を通過する（３時間前）を表している。

　　ｙ＝６χ の χ に－３を代入するとｙ＝６×（－３）＝－１８

　これはＡ地点を通過する３時間前にはＡ地点から西へ１８㎞の位置にいたことを表している。

■比例を表す式・・・y が χ の関数で、y ＝ a χ という式で表されるとき、ｙは χ に比例するという。
■比例定数・・・・・一定の数やそれを表す文字を定数という。
　　　　　　　　　　比例を表す式ｙ＝ a χ 文字 a は定数であり、比例定数という。
　　　　　　　　　　比例の関係 ｙ＝ a χ を、関数ｙ＝ a χ ともいう。

（例）

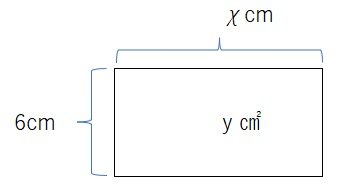
縦が６㎝、横がχ㎝の長方形の面積をｙ㎠とする。このとき、χとｙの関係を式に表すと　　ｙ＝６χ
したがってｙはχに比例し比例定数は６である。


χとｙの関係は下記の表のようになり次のことがわかる。
χの値が２倍、３倍、４倍、・・・となるとそれに伴いｙの値も２倍、３倍、４倍、・・・になっている。


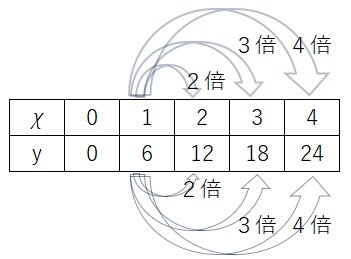
χ ≠ ０のとき、ｙ/ χ の値はいつも６になり比例定数に等しい。

（例題）（１）
ある薬品は、液体Ａを３０㎖、液体Ｂを７０㎖混ぜて作られている。液体Ａが１２㎖あるとき、この薬品を作るには液体Ｂを何㎖混ぜればよいか。

（解答）
この薬品を作るとき液体Ａと液体Ｂの量の比は、（液体Ａ）：（液体Ｂ）＝３０：７０だから、この比に等しくなるようにすればよい。
液体Ｂをχ㎖混ぜるとすると、
　　　　　　　１２： χ ＝３０：７０
　　　　　　　χ × ３０ ＝１２×７０
　　　 　　　　３０χ　＝　８４０
　　　　　 　　　　χ　＝　２８　　　　∴　２８㎖　


（例題）（２）
あるクラスの生徒数は３５人で、男子と女子の人数の比は４：３である。このクラスの男子は何人か。

（解答）
男子と女子の人数の比が４：３だから、全体は７となる。
男子がχ人だとすると
　　　　　　　　χ ：３５＝４：７
　　　　　　　　χ × ７　＝３５×４
　　　　　　　　　７χ　 ＝　１４０
　　　　　　　　　　χ　 ＝　２０　　　∴　２０人

（例題）
あるイベントの参加者のうち、中学生と高校生は合わせて２００人で、中学生の参加者は高校生の参加者の６０％より８人多かったという。このイベントに参加した中学生は何人か。

（解答）
・中学生の参加者を χ人とすると、高校生の参加者は（２００ー χ）人
・中学生の参加者は高校生の参加者の６０％より８人多いから、
　　　χ ＝６０/１００（２００ー χ)＋８　　　※ a人の６０％⇒ a × ６０/１００
　１０χ ＝６（２００ーχ）＋８０
　これを解くと
　　　χ ＝８０（人）

　∴　８０人