2023.10.25
2023.10.24
2023.10.23
2023.10.19
3⃣ 2点の座標がわかるとき
(例題)
yは χ の一次関数で、そのグラフが2点(1,3)、(3,7)を通る直線であるとき、この一次関数の式を求めなさい。
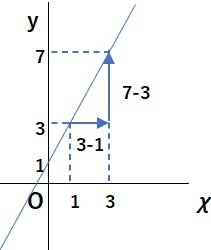
(解き方1)
求める一次関数の式をy=a χ +bとする。
2点(1,3)、(3,7)を通るから、
傾き a は、
 まず傾きを求める。
まず傾きを求める。
だから y=2χ+b
グラフは、点(1,3)を通るから
3=2×1+b
b=1
答 y=2χ+1
(解き方2)
求める一次関数の式をy=a χ +bとする。
χ=1のときy=3だから、3= a + b・・・・①
χ=3のときy=7だから、7= 3a + b・・・②
①、②を連立方程式とみて解くと、 a、bについての連立方程式を
(a ,b)=(2,1) つくる
答 y=2χ+1
(例題)
yは χ の一次関数で、そのグラフが2点(1,3)、(3,7)を通る直線であるとき、この一次関数の式を求めなさい。
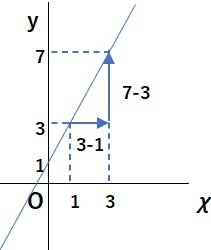
(解き方1)
求める一次関数の式をy=a χ +bとする。
2点(1,3)、(3,7)を通るから、
傾き a は、
だから y=2χ+b
グラフは、点(1,3)を通るから
3=2×1+b
b=1
答 y=2χ+1
(解き方2)
求める一次関数の式をy=a χ +bとする。
χ=1のときy=3だから、3= a + b・・・・①
χ=3のときy=7だから、7= 3a + b・・・②
①、②を連立方程式とみて解くと、 a、bについての連立方程式を
(a ,b)=(2,1) つくる
答 y=2χ+1
2023.10.17