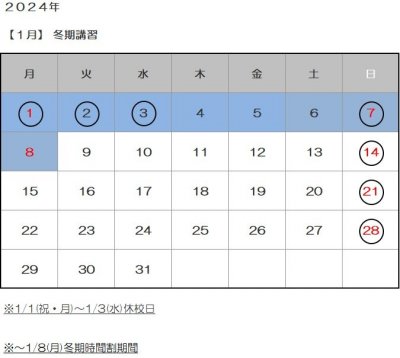
2023.12.28
2023.12.26
2023.12.22
2023.12.19
2023.12.16
3⃣ 逆
■逆・・・ある定理の仮定と結論を入れ替えたものを、その定理の逆という。あることがらが正しくても、その逆は正しいとは限らない。
(例)
(1)自然数 a が4の倍数ならば a は偶数である。
(2)自然数 a が偶数ならば a は4の倍数である。
(2)は(1)の逆であり、(1)は(2)の逆である。
また、(1)は正しいが、(2)は正しくない。たとえば6は偶数であるが、4の倍数ではない。このような成り立たない例を反例という。あることがらが正しくないことを示すには、反例を示せばよい。
〇〇〇ならば▢▢▢である。
逆 ↓ ↑逆
▢▢▢ならば〇〇〇である。
■逆・・・ある定理の仮定と結論を入れ替えたものを、その定理の逆という。あることがらが正しくても、その逆は正しいとは限らない。
(例)
(1)自然数 a が4の倍数ならば a は偶数である。
(2)自然数 a が偶数ならば a は4の倍数である。
(2)は(1)の逆であり、(1)は(2)の逆である。
また、(1)は正しいが、(2)は正しくない。たとえば6は偶数であるが、4の倍数ではない。このような成り立たない例を反例という。あることがらが正しくないことを示すには、反例を示せばよい。
〇〇〇ならば▢▢▢である。
逆 ↓ ↑逆
▢▢▢ならば〇〇〇である。