2023.11.27
2023.11.23
2023.11.22
2⃣ 合同条件を使った証明の進め方
(例題)
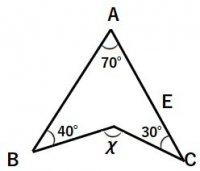
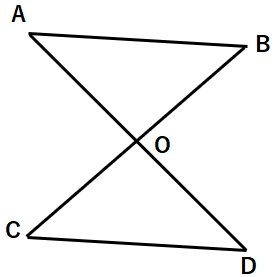
右の図で、AB∥CD、AB=CDならばAO=DO
となる。このことを証明するとき、次の問い
に答えなさい。
(1)結論AO=DOを導くには、どの三角形
とどの三角形の合同を示せばよいか。
(2)(1)であげた2つの三角形で、等し
い辺、等しい角はどれか。
(3)(2)から、(1)で考えた2つの三
角形の合同を示すには、三角形の合同条件の
どれを使えばよいか。
(解き方)
線分の長さや角が等しいことを証明するのに、三角形の合同条件を使うことが多い。
合同な図形では、対応する線分の長さや角の大きさは等しい。
(1)△AOBと△DOCが合同であることがわかれば、対応する辺の長さが
等しいから AO=DO がいえる。
答 △AOBと△DOC
(2)仮定より、AB=DC
AB∥CDで錯角は、等しいから
∠OAB=∠ODC
∠OBA=∠OCD
答 AB=DC、∠OAB=∠ODC、∠OBA=∠OCD
(3)(2)の3つの条件から、1組の辺とその両端の角が、それぞれ等しいので、 △AOB ≡ △DOC がいえる。
答 1組の辺とその両端の角が、それぞれ等しい。

(例題)
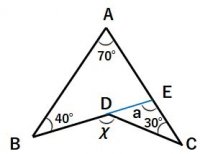
右の図で、AB∥CD、AB=CDならばAO=DO
となる。このことを証明するとき、次の問い
に答えなさい。
(1)結論AO=DOを導くには、どの三角形
とどの三角形の合同を示せばよいか。
(2)(1)であげた2つの三角形で、等し
い辺、等しい角はどれか。
(3)(2)から、(1)で考えた2つの三
角形の合同を示すには、三角形の合同条件の
どれを使えばよいか。
(解き方)
線分の長さや角が等しいことを証明するのに、三角形の合同条件を使うことが多い。
合同な図形では、対応する線分の長さや角の大きさは等しい。
(1)△AOBと△DOCが合同であることがわかれば、対応する辺の長さが
等しいから AO=DO がいえる。
答 △AOBと△DOC
(2)仮定より、AB=DC
AB∥CDで錯角は、等しいから
∠OAB=∠ODC
∠OBA=∠OCD
答 AB=DC、∠OAB=∠ODC、∠OBA=∠OCD
(3)(2)の3つの条件から、1組の辺とその両端の角が、それぞれ等しいので、 △AOB ≡ △DOC がいえる。
答 1組の辺とその両端の角が、それぞれ等しい。
2023.11.21
2023.11.20
1⃣ 証明のしくみ
■仮定と結論・・・「〇〇〇ならば▢▢▢である。」という形で述べられることがらの、〇〇〇の部分を仮定、▢▢▢の部分を結論という。
〇〇〇ならば▢▢▢である
↑ ↑
仮定 結論
■証明・・・すでに正しいと認められていることがらを根拠として、仮定から結論を導くことを証明という。
【仮定】
↓ ←正しいと認められたことがら
【結論】
■証明のしくみ・・・証明は次の手順で行う。
① 仮定から出発し、
② すでに正しいと認められたことがらを根拠に使って、
③ 結論を導く。
■仮定と結論・・・「〇〇〇ならば▢▢▢である。」という形で述べられることがらの、〇〇〇の部分を仮定、▢▢▢の部分を結論という。
〇〇〇ならば▢▢▢である
↑ ↑
仮定 結論
■証明・・・すでに正しいと認められていることがらを根拠として、仮定から結論を導くことを証明という。
【仮定】
↓ ←正しいと認められたことがら
【結論】
■証明のしくみ・・・証明は次の手順で行う。
① 仮定から出発し、
② すでに正しいと認められたことがらを根拠に使って、
③ 結論を導く。