2023.08.31
【休校日】
日曜日・・・３日、１０日、１７日、２３日、２４日
→教室への入室はできません
【受付時間】
通常期間 15：00～20：00（電話受付は常時応対）
→休校日を除く
2023.08.30
■円周率・・・円周率は、円周の直径に対する割合でギリシャ文字π（パイ）で表す。
π＝3.1415926535･･･
■円の周の長さと面積の公式
半径ｒの円の周の長さをℓ、面積をＳとすると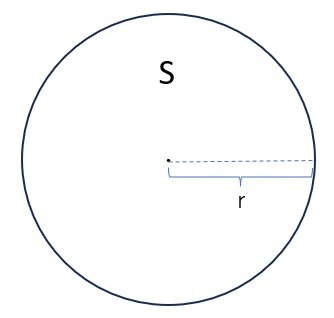
ℓ＝２πｒ
Ｓ＝ πｒ²
（例）半径３㎝の円の周の長さℓと面積Ｓは、
ℓ＝２π×３＝６π（㎝）
Ｓ＝ π×３²＝９π（㎠）
■おうぎ形の弧の長さや面積と中心角の関係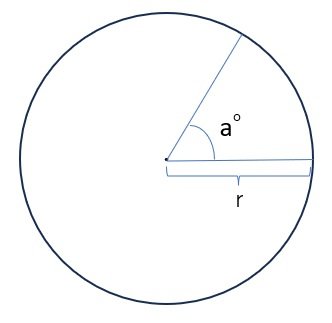
同じおうぎ形の弧の長さや面積は中心角に比例
する。
したがって、中心角 a °のおうぎ形の弧の長さや
面積は 円の周の長さや面積の a / 360倍となる。
■おうぎ形の弧の長さや面積の公式
半径ｒ、中心角 a °のおうぎ形の弧の長さℓ、
面積Ｓとすると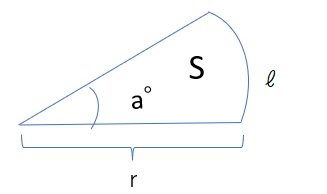
ℓ＝２πｒ× a / 360
Ｓ＝ πｒ²× a / 360
（例）半径５㎝、中心角72°のおうぎ形の弧の
長さℓと面積Ｓは、
ℓ＝２π ×５× 72 / 360＝２π（㎝）
Ｓ＝ π ×５²× 72 / 360＝５π（㎠）
π＝3.1415926535･･･
■円の周の長さと面積の公式
半径ｒの円の周の長さをℓ、面積をＳとすると
ℓ＝２πｒ
Ｓ＝ πｒ²
（例）半径３㎝の円の周の長さℓと面積Ｓは、
ℓ＝２π×３＝６π（㎝）
Ｓ＝ π×３²＝９π（㎠）
■おうぎ形の弧の長さや面積と中心角の関係
同じおうぎ形の弧の長さや面積は中心角に比例
する。
したがって、中心角 a °のおうぎ形の弧の長さや
面積は 円の周の長さや面積の a / 360倍となる。
■おうぎ形の弧の長さや面積の公式
半径ｒ、中心角 a °のおうぎ形の弧の長さℓ、
面積Ｓとすると
ℓ＝２πｒ× a / 360
Ｓ＝ πｒ²× a / 360
（例）半径５㎝、中心角72°のおうぎ形の弧の
長さℓと面積Ｓは、
ℓ＝２π ×５× 72 / 360＝２π（㎝）
Ｓ＝ π ×５²× 72 / 360＝５π（㎠）
2023.08.28
（例題）
点Pは、右の図のような長方形ABCDの辺BC上を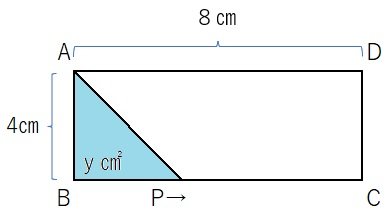
BからCまで動く。BPをχ㎝、三角形ABPの面積を
ｙ㎠とする。
（１）χとｙの関係を式に表しなさい。またχの変域を答えなさい。
（２）χとｙの関係を表わすグラフを書きなさい。
（３）面積が10㎠になるときのBPの長さを求めなさい。
（解答）
（１）BPを底辺とみると高さはABだから
ｙ＝１/２× χ × 4
よってｙ＝２χ
BCは８㎝だからχの変域は、
０≦ χ ≦ ８
∴ ｙ＝２χ、０≦ χ ≦ ８
（２）χ＝０のときｙ＝０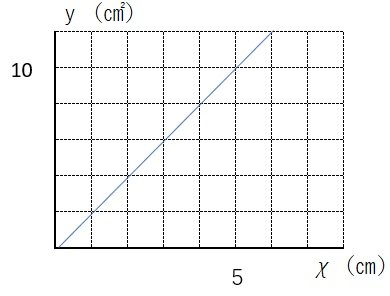
χ＝８のときｙ＝16
グラフは原点と点（８,１６）
を結ぶ直線 ∴ 右図
（３）ｙ＝２χにｙ＝10を代入して
10＝２χ
χ＝ ５
∴ ５㎝
点Pは、右の図のような長方形ABCDの辺BC上を
BからCまで動く。BPをχ㎝、三角形ABPの面積を
ｙ㎠とする。
（１）χとｙの関係を式に表しなさい。またχの変域を答えなさい。
（２）χとｙの関係を表わすグラフを書きなさい。
（３）面積が10㎠になるときのBPの長さを求めなさい。
（解答）
（１）BPを底辺とみると高さはABだから
ｙ＝１/２× χ × 4
よってｙ＝２χ
BCは８㎝だからχの変域は、
０≦ χ ≦ ８
∴ ｙ＝２χ、０≦ χ ≦ ８
（２）χ＝０のときｙ＝０
χ＝８のときｙ＝16
グラフは原点と点（８,１６）
を結ぶ直線 ∴ 右図
（３）ｙ＝２χにｙ＝10を代入して
10＝２χ
χ＝ ５
∴ ５㎝
2023.08.25
（例題）
兄と弟が同時に家を出発し家から６００ｍ離れた駅に行く。兄は分速１００ｍ、弟は分速７５ｍで歩く。家を出発してからχ（分後）に家からｙ（ｍ）離れているとして次の問いに答えなさい。
（１）兄と弟のそれぞれについてχとｙの関係を式に表しなさい。またそのグラフを書きなさい。
（２）兄と弟が１００ｍ離れるのは、家を出発してから何分後か。
（３）兄が駅に着いたとき、弟は駅まであと何ｍのところにいるか。
（解答）
（１）（道のり）＝（速さ）×（時間）より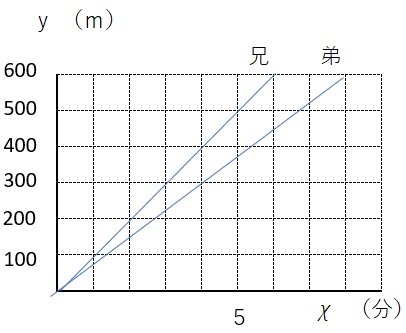
兄の式はｙ＝１００χ
弟の式はｙ＝７５χ
∴ 兄・・ｙ＝１００χ 、弟・・ｙ＝７５χ
（２）２つのグラフのｙ座標の差が１００になるときのχ座標は４だから、４分後
∴ ４分後
（３）６分後（χ＝６）のとき2つのグラフのｙ座標の差は１５０だから、弟は駅まであと１５０ｍのところにいる。
∴ １５０ｍ
兄と弟が同時に家を出発し家から６００ｍ離れた駅に行く。兄は分速１００ｍ、弟は分速７５ｍで歩く。家を出発してからχ（分後）に家からｙ（ｍ）離れているとして次の問いに答えなさい。
（１）兄と弟のそれぞれについてχとｙの関係を式に表しなさい。またそのグラフを書きなさい。
（２）兄と弟が１００ｍ離れるのは、家を出発してから何分後か。
（３）兄が駅に着いたとき、弟は駅まであと何ｍのところにいるか。
（解答）
（１）（道のり）＝（速さ）×（時間）より
兄の式はｙ＝１００χ
弟の式はｙ＝７５χ
∴ 兄・・ｙ＝１００χ 、弟・・ｙ＝７５χ
（２）２つのグラフのｙ座標の差が１００になるときのχ座標は４だから、４分後
∴ ４分後
（３）６分後（χ＝６）のとき2つのグラフのｙ座標の差は１５０だから、弟は駅まであと１５０ｍのところにいる。
∴ １５０ｍ
2023.08.24
（例題）
くぎ１５本の重さを測ったら３６ｇであった。同じくぎが２４０ｇあるとき、くぎは全部で何本あると考えられるか。
（解答）
くぎの本数は重さに比例すると考えられるから、重さχｇのくぎの本数をｙ本とするとｙ＝a χ と表すことができる。
χ＝３６のときｙ＝１５だから
１５＝a × ３６
a ＝１５/３６＝５/１２
よって、ｙ＝５χ /１２
この式にχ＝２４０を代入して
ｙ＝５/１２×２４０＝１００ ∴ １００本
※比例の関係では、一方が２倍、３倍、・・・になると他方も２倍、３倍、・・・になる。これを利用して重さが２４０÷３６＝２０/３倍だから本数も２０/３倍と考えると
１５×２０/３＝１００（本）
くぎ１５本の重さを測ったら３６ｇであった。同じくぎが２４０ｇあるとき、くぎは全部で何本あると考えられるか。
（解答）
くぎの本数は重さに比例すると考えられるから、重さχｇのくぎの本数をｙ本とするとｙ＝a χ と表すことができる。
χ＝３６のときｙ＝１５だから
１５＝a × ３６
a ＝１５/３６＝５/１２
よって、ｙ＝５χ /１２
この式にχ＝２４０を代入して
ｙ＝５/１２×２４０＝１００ ∴ １００本
※比例の関係では、一方が２倍、３倍、・・・になると他方も２倍、３倍、・・・になる。これを利用して重さが２４０÷３６＝２０/３倍だから本数も２０/３倍と考えると
１５×２０/３＝１００（本）
2023.08.18
■ｙがχに反比例するとき、１組のχ , ｙの値からχとｙの関係を式に表す事ができる。
（例）ｙは、χに反比例し、χ＝４のときｙ＝６である。
（１）χとｙの関係を式に表す。
比例定数を a とすると、ｙ＝a / χと表すことができる。
χ＝４のときｙ＝６であるから、
６＝ a / ４
a ＝ ２４
したがってｙ＝２４/χ
（２）χ＝－３のときよ値を求める。
（１）で求めた式にχ＝－３を代入すると、
ｙ＝２４/ －３
＝－８
（例）ｙは、χに反比例し、χ＝４のときｙ＝６である。
（１）χとｙの関係を式に表す。
比例定数を a とすると、ｙ＝a / χと表すことができる。
χ＝４のときｙ＝６であるから、
６＝ a / ４
a ＝ ２４
したがってｙ＝２４/χ
（２）χ＝－３のときよ値を求める。
（１）で求めた式にχ＝－３を代入すると、
ｙ＝２４/ －３
＝－８
2023.08.09
■反比例を表す式・・・ｙがχの関数で、ｙ＝a / χ という式で表されるとき、ｙはχに反比例するという。
■比例定数・・・・反比例を表す式ｙ＝a / χ で、定数 a を比例定数という。反比例の関係ｙ＝a / χ を、関数ｙ＝a / χ ともいう。ｙがχに反比例するとき、χとｙの積χｙの値は一定で、比例定数に等しい。
（例）６０㎝のひもをχ等分するときの１本の長さをｙ㎝とすると、
ｙ＝６０/ χ
したがって、ｙはχに反比例する。
比例定数は６０で、もとのひもの長さである。
χとｙの関係は下の表のようになり、次のことがわかる。
（１）χの値が2倍、3倍、4倍・・・になるとそれにともなってｙの値は
1/2倍、1/3倍、1/4倍・・・となっている。
（２）χｙの値は、いつも６０になり、比例定数に等しい。
■比例定数・・・・反比例を表す式ｙ＝a / χ で、定数 a を比例定数という。反比例の関係ｙ＝a / χ を、関数ｙ＝a / χ ともいう。ｙがχに反比例するとき、χとｙの積χｙの値は一定で、比例定数に等しい。
（例）６０㎝のひもをχ等分するときの１本の長さをｙ㎝とすると、
ｙ＝６０/ χ
したがって、ｙはχに反比例する。
比例定数は６０で、もとのひもの長さである。
χとｙの関係は下の表のようになり、次のことがわかる。
（１）χの値が2倍、3倍、4倍・・・になるとそれにともなってｙの値は
1/2倍、1/3倍、1/4倍・・・となっている。
（２）χｙの値は、いつも６０になり、比例定数に等しい。
2023.08.08
2023.08.08
■比例のグラフの特徴 ｙ＝a χ のグラフは原点を通る直線である。
①a>0のとき
右上がりの直線
χの値が増加すると
ｙの値も増加する。
②a<0のとき
右下がりの直線
χの値が増加すると
ｙの値は減少する。
■グラフから比例の式を求める。
比例の式はｙ＝a χ と表されるから、これにグラフが通る点の座標を代入して、aの値を求める。
（例題）
右の図の比例のグラフは点（４,３）を通るから
χ＝４のとき、ｙ＝３である。
これをｙ＝a χ に代入すると
３＝ a × ４
a ＝ ３/４
したがってｙ＝３/４ χ
①a>0のとき
右上がりの直線
χの値が増加すると
ｙの値も増加する。
②a<0のとき
右下がりの直線
χの値が増加すると
ｙの値は減少する。
■グラフから比例の式を求める。
比例の式はｙ＝a χ と表されるから、これにグラフが通る点の座標を代入して、aの値を求める。
（例題）
右の図の比例のグラフは点（４,３）を通るから
χ＝４のとき、ｙ＝３である。
これをｙ＝a χ に代入すると
３＝ a × ４
a ＝ ３/４
したがってｙ＝３/４ χ
2023.08.04
■ｙがχに比例するとき、１組のχ ,ｙの値からχとｙの関係を式に表すことができる。
（例題）
（１）ｙはχに比例しχ＝３のときｙ＝－２１である。
χとｙの関係を式に表すと比例定数をaとしてｙ＝a χと表すことができる。
χ＝３のとき、ｙ＝ー２１であるから
ー２１＝a × ３
a ＝ー７
したがってｙ＝ー７χ
（２）χ＝ー５のときのｙを求める。
（１）で求めた式にχ＝ー５を代入すると
ｙ＝ー７×（ー５）
ｙ＝３５
（例題）
（１）ｙはχに比例しχ＝３のときｙ＝－２１である。
χとｙの関係を式に表すと比例定数をaとしてｙ＝a χと表すことができる。
χ＝３のとき、ｙ＝ー２１であるから
ー２１＝a × ３
a ＝ー７
したがってｙ＝ー７χ
（２）χ＝ー５のときのｙを求める。
（１）で求めた式にχ＝ー５を代入すると
ｙ＝ー７×（ー５）
ｙ＝３５