2024.02.29
2⃣ 箱ひげ図の書き方
■ 箱ひげ図の書き方
(例題)
上の表は、10人の生徒が1ヵ月間に図書館に行った日数を記録したものである。次の問いに答えなさい。
(1) データの最小値、最大値、四分位数を求めなさい。
(2) データの箱ひげ図をかきなさい。
(解き方)
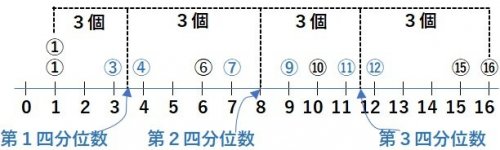
(1) データを小さい方から順に並べ、小さい方と大きい方の半分ずつに分ける。
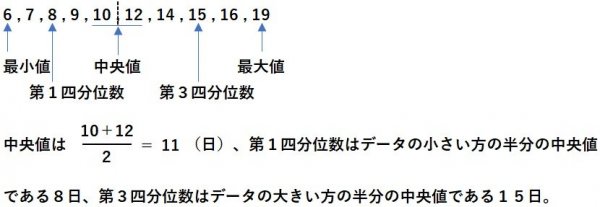
答 最小値6日、最大値19日、第1四分位数8日、中央値11日、第3四分位数15日
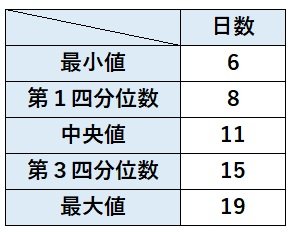
(2) 数直線をかき、最小値6、第1四分位数8、中央値11、第3四分位数15、最大値19の位置に線をかく。次に箱とひげ図をかく。
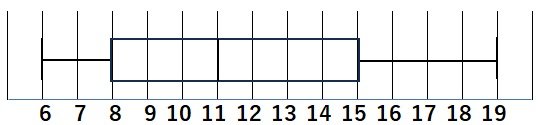
※データが奇数個の場合は、小さい順に並べた中央の1個のデータ(中央値)を除き、小さい方の半分、大きい方の半分の中央値が、それぞれ第1四分位数、第3四分位数になる。
■ 箱ひげ図の書き方

(例題)
上の表は、10人の生徒が1ヵ月間に図書館に行った日数を記録したものである。次の問いに答えなさい。
(1) データの最小値、最大値、四分位数を求めなさい。
(2) データの箱ひげ図をかきなさい。
(解き方)
(1) データを小さい方から順に並べ、小さい方と大きい方の半分ずつに分ける。

答 最小値6日、最大値19日、第1四分位数8日、中央値11日、第3四分位数15日

(2) 数直線をかき、最小値6、第1四分位数8、中央値11、第3四分位数15、最大値19の位置に線をかく。次に箱とひげ図をかく。

※データが奇数個の場合は、小さい順に並べた中央の1個のデータ(中央値)を除き、小さい方の半分、大きい方の半分の中央値が、それぞれ第1四分位数、第3四分位数になる。