2023年12月の記事一覧 | 東大宮教室 | 個別指導塾・学習塾【城南コベッツ】

図形の性質と証明②（中２）

2023.12.15

2⃣ 二等辺三角形になるための条件

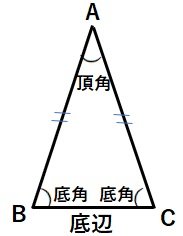
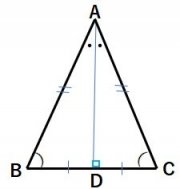
■二等辺三角形になるための条件・・・三角形の２つの角が等しければ、その三角形は、等しい２つの角を底角とする二等辺三角形である。

※ある三角形が二等辺三角形であることを示すには、

　　　1⃣　２つの辺が等しい。　　　　2⃣　２つの角が等しい。

　のどちらかをいえばよい。

1⃣ 二等辺三角形の性質

■定義・・・言葉の意味をはっきり述べたものを定義という。

■定理・・・証明されたことがらのうち、基本になるものを定理という。

■二等辺三角形・・２つの辺が等しい三角形を二等辺三角形という。（定義）
　　　二等辺三角形で、　　　　　　　　　
　　　　　長さの等しい辺のつくる角を頂角
　　　　　頂角に対する辺を底辺　　　　　
　　　　　底辺の両端の角を底角　　　　　
　　　という。　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　
※「対する」は「向かい合う」の意味。

■二等辺三角形の性質

　1⃣ 二等辺三角形の２つの底角は等しい。（定理）
　2⃣ 二等辺三角形の頂角の二等分線は、底辺を垂直に２等分する。（定理）　　　　　　　　　　　　　　　　
　（例）AB＝ACの二等辺三角形ABCで
　　１⃣　∠B＝∠C　　　　　　　　　　
　　2⃣　ADが∠Aの二等分線ならば、　
　　　　　　AD⊥BC　　　　　　　　
　　　　　　BD＝CD　　　　　　　　
　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　

大学最前線Vol.36（薬学部と薬剤師）

2023.12.08

１２月カレンダーのお知らせ（休校日）

2023.12.06

【休校日】
日曜日・・・３日、１０日、１７日、２４日、３１日
金曜日・・・２９日
土曜日・・・３０日
→ 教室への入室はできません

【受付時間】
通常期間　15：00～20：00（電話受付は常時応対）
→ 休校日を除く

角の大きさの求め方④（中２）

2023.12.05

4⃣ 三角形と角の二等分線
　　　　　　　　　　　　　　　　　　　　　　
（例題）　　　　　　　　　　　　　　　　　　
右の図のように、△ABCの∠B、∠Cの二等分線の
交点をIとするとき、∠BICの大きさを求めなさい。
　　　　　　　　　　　　　　　　　　　　　　
（解き方）　　　　　　　　　　　　　　　　　
∠IBC＝∠b、∠ICB＝∠cとして、２つの三角形ABC、
IBCの内角の和を考える。　　　　　　　　　　　
△ABCにおいて、∠ABC＝２∠b、∠ACB＝２∠cだから、
　　　　　８０°＋２∠b＋２∠c＝１８０°
　　　　　　　　　　 ∠b＋∠c＝９０°
△IBCにおいて、∠BIC＝１８０°－（∠b＋∠c）
　　　　　　　　　　＝１８０°－５０°
　　　　　　　　　　＝１３０°
　　　　　　　　　　　　　　　　　　　　　　　　　答　１３０°　

城南コベッツ東大宮教室

図形の性質と証明②（中２）

図形の性質と証明①（中２）

大学最前線Vol.36（薬学部と薬剤師）

１２月カレンダーのお知らせ（休校日）

角の大きさの求め方④（中２）

新着情報

カレンダー

アーカイブ