2023.10.14
2023.10.13
2023.10.12
2023.10.11
2023.10.10
2⃣ 一次関数の値の変化
■変化の割合・・χ の増加量に対するyの増加量の割合を変化の割合という。
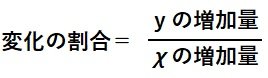 (例)一次関数y=3χ-2でχ の値が2から5まで増加したとき、
(例)一次関数y=3χ-2でχ の値が2から5まで増加したとき、
χ=2のとき、y=3×2-2=4
χ=5のとき、y=3×5-2=13

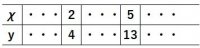
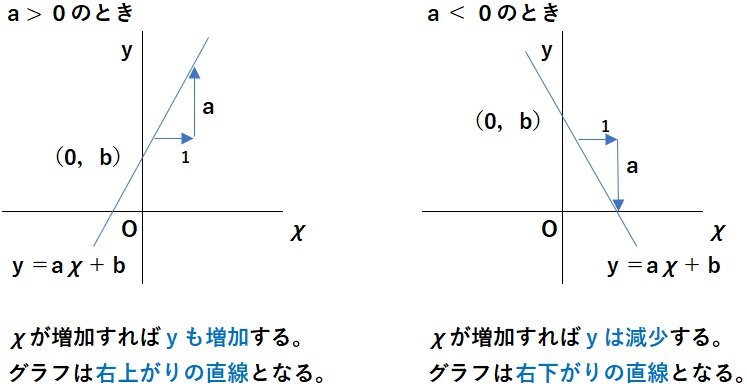
■一次関数の変化の割合・・・一次関数y=a χ + bでは変化の割合は一定で、a に等しい。
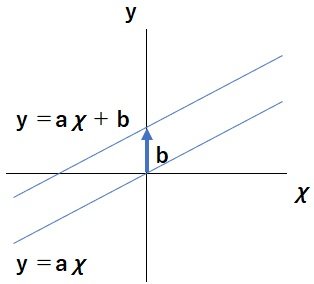
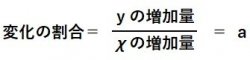 y=a χ + b
y=a χ + b
↑
変化の割合
この式から次の式が成り立つ。
yの増加量= a × χ の増加量
※一定の値 a は、χ が1だけ増加したときのyの増加量である。
※反比例の関数y= a / χでは変化の割合は一定にならない。
(例)一次関数y=3χ-2について
・変化の割合は、3
・χ の増加量が4のとき、yの増加量は3×4=12
■変化の割合・・χ の増加量に対するyの増加量の割合を変化の割合という。
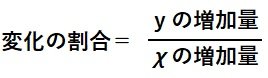 (例)一次関数y=3χ-2でχ の値が2から5まで増加したとき、
(例)一次関数y=3χ-2でχ の値が2から5まで増加したとき、χ=2のとき、y=3×2-2=4
χ=5のとき、y=3×5-2=13
■一次関数の変化の割合・・・一次関数y=a χ + bでは変化の割合は一定で、a に等しい。
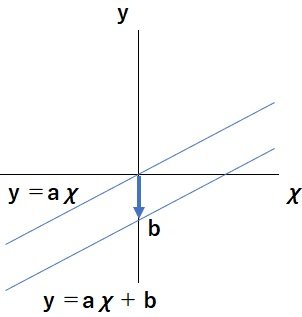
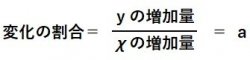 y=a χ + b
y=a χ + b↑
変化の割合
この式から次の式が成り立つ。
yの増加量= a × χ の増加量
※一定の値 a は、χ が1だけ増加したときのyの増加量である。
※反比例の関数y= a / χでは変化の割合は一定にならない。
(例)一次関数y=3χ-2について
・変化の割合は、3
・χ の増加量が4のとき、yの増加量は3×4=12