2026.01.29
証明問題は「書く」前に「描く」
数学の証明問題において、「条件は覚えているのに証明が書けない」という悩みは非常に多く聞かれます。
しかし、その原因は才能や記憶力ではありません。
「問題文を頭の中だけで処理しようとしていること」にあります。
今回は、典型的な例題を通して、図を活用した「証明の書き方」を解説します。
この問題をどう解くか？
【問題例】
△ABCにおいて、点Dは辺BC上にあり、ADは∠Aの二等分線である。
また、AB=ACであるとき、△ABD≡△ACDであることを証明しなさい。
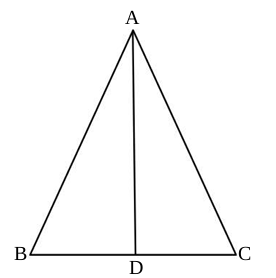この問題、文章だけを眺めていても「何から書けばいいか」は見えてきません。
多くの生徒がここで「二等分線ってどう書くんだっけ？」「対応する順番は？」と考えることが多くなってしまいます。
なぜ「図に書き込む」だけで解けるようになるのか
多くの生徒が証明でつまずく最大の理由は、
「問題文」と「合同条件」を頭の中だけで結びつけようとするから
です。
問題文を読みながら「AB=ACで、角の二等分線だから......」と文字で考えていると、脳は情報の処理だけで手一杯になります。
しかし、図に印（|| や ●）を書き込むことで、脳は「言葉」を処理するモードから、
直感的に形を捉える「図形」モードに切り替わります。
図に書き込むメリットは3つあります。
- 情報の整理： 仮定（問題で与えられたヒント）がひと目でわかる。
- 「隠れた条件」の発見： 共通な辺や対頂角など、問題文に書かれていない事実に気づきやすくなる。
- 合同条件の選択： 印がついた場所を見るだけで、3つの合同条件のうちどれを使うべきかが自然に浮かび上がる。
合同の証明を完成させる「4ステップ」
では、例題をもとに、実際にどのような手順で思考を進めればよいか整理してみましょう。
①仮定を図に反映させる
まずは問題文のテキストを「記号」に置き換えます。
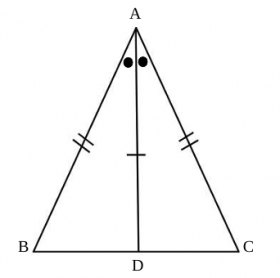
- 「AB=AC」→ 辺ABとACに、同じ本数の印（||）を入れる。
- 「ADは∠Aの二等分線」→ ∠BADと∠CADに、同じ印（●）を入れる。
- ここで重要！ 「隠れた条件」を探す。この図では、ADが2つの三角形の「壁」になっています。
②比べる三角形を宣言する
図を見ると、左側の△ABDと右側の△ACDが重なり合っていることがわかります。
「これからこの2つを比べますよ」という合図として、証明の書き出しを固定します。
△ABDと△ACDにおいて、
③根拠を3つ並べる
図につけた印を、そのまま数式に書き起こします。
このとき、「なぜそれが言えるのか」という理由（仮定より、など）を添えるのがルールです。
-
AB = AC （仮定より）
-
∠BAD = ∠CAD （角の二等分線なので）
-
AD = AD （共通な辺なので）
④合同条件に当てはめる
3つの証拠が出揃ったら、図をもう一度見ます。
「辺・角・辺」の順に印が並んでいるはずです。
ここで初めて、暗記していた合同条件を当てはめます。
2組の辺とその間の角がそれぞれ等しい
このフレーズが決まれば、あとは「したがって、△ABD ≡ △ACD」と結ぶだけです。
証明のテンプレート
書き方に迷ったら、以下の「型」に流し込んでみてください。
【証明】
△ABDと△ACDにおいて、仮定より、 AB = AC ......①
ADは∠Aの二等分線なので、 ∠BAD = ∠CAD ......②
また、ADは共通の辺なので、 AD = AD ......③①、②、③より、 2組の辺とその間の角がそれぞれ等しい。
したがって △ABD ≡ △ACD
ケアレスミスを防ぐ「対応順」のコツ
最後に、多くの生徒が最後に減点されるポイントが「対応する頂点の順番」です。
図に書き込みをしていれば、このミスも防げます。
例えば、△ABDに対応するのは、△ACDなのか、△ADCなのか。
図の印を辿ってみましょう。
「辺（||）を通って、角（●）を通る」というルートで名前を呼べば、
左が「A→B→D」なら、右も同じルートで「A→C→D」になると一発でわかります。
まとめ：証明問題は「文章題」ではなく「パズル」
証明問題を「文章題」だと捉えると、「どんな言葉を使えばいいのか」「どう作文すればいいのか」という悩みにはまってしまいます。しかし、その正体は
「ピース（仮定・条件）を組み合わせて、
指定された形（結論）を完成させるパズル」
です。
- 図に印をつける（思考の視覚化）
- 3つの証拠を並べる（パズルのピース集め）
- 合同条件を選ぶ（パズルの完成）
このリズムを身につければ、どんなに複雑な図形が出てきても、迷うことなくペンを動かせるようになります。
まずは、手元の問題集の図に「●」や「||」を書き込むことから始めてみましょう。
