2023.09.26
2023.09.25
2023.09.22
2023.09.21
2⃣ 加減法(1)
(例題)
(1) (2)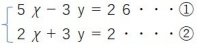
絶対値が等しく、符号も等しい係数 絶対値が等しく、符号が反対
に着目して上の式から下の式を引い の係数に着目して、2式を加
てyだけの式にする。 えてχだけの式にする。
①-②より、 ①+②より、
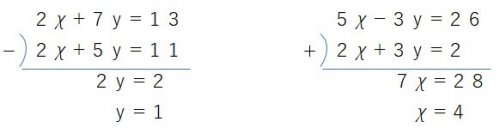
y=1を代入すると、 χ=4を代入すると、
2χ+5×1=11 2×4+3y=2
2χ=6 3y=-6
χ=3 y=-2
答(χ , y)=(3,1) 答(χ , y)=(4,-2)
⇒文字 χ を含む2つの方程式から、χ を含まない1つの方程式をつくることを χ を消去するという。
また、このように左辺どうし、右辺どうしをそれぞれ、たすかひくかして1つの文字を消去して解く方法を加減法という。
(例題)
(1) (2)
絶対値が等しく、符号も等しい係数 絶対値が等しく、符号が反対
に着目して上の式から下の式を引い の係数に着目して、2式を加
てyだけの式にする。 えてχだけの式にする。
①-②より、 ①+②より、
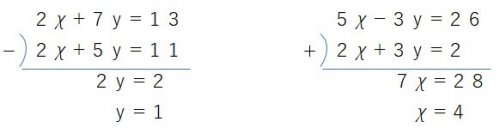
y=1を代入すると、 χ=4を代入すると、
2χ+5×1=11 2×4+3y=2
2χ=6 3y=-6
χ=3 y=-2
答(χ , y)=(3,1) 答(χ , y)=(4,-2)
⇒文字 χ を含む2つの方程式から、χ を含まない1つの方程式をつくることを χ を消去するという。
また、このように左辺どうし、右辺どうしをそれぞれ、たすかひくかして1つの文字を消去して解く方法を加減法という。
2023.09.20
1⃣ 連立方程式とその解
■二元一次方程式・・2つの文字を含む一次方程式を二元一次方程式という。
(例)χ+y=10は二元一次方程式である。
χ , yを0以上の整数とするとき、χ , yの値の組は次の表のようになる。
■二元一次方程式の解・・二元一次方程式の成り立たせる文字の値の組を、その方程式の解という。
※二元一次方程式の解は無数にある。
■連立方程式・・2つ以上の方程式を組み合わせたものを連立方程式という。
■連立方程式の解・・連立方程式のどの方程式も成り立たせるような文字の値の組を連立方程式の解といい、解を求めることを連立方程式を解くという。
(例)下記の連立方程式について上の表は、①を成り立たせるχ , yの値の組であり、このうち、②も成り立たせるものは、χ=6, y=4である。
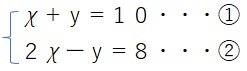
したがって、この連立方程式の解は、(χ , y)=(6, 4)
■二元一次方程式・・2つの文字を含む一次方程式を二元一次方程式という。
(例)χ+y=10は二元一次方程式である。
χ , yを0以上の整数とするとき、χ , yの値の組は次の表のようになる。
■二元一次方程式の解・・二元一次方程式の成り立たせる文字の値の組を、その方程式の解という。
※二元一次方程式の解は無数にある。
■連立方程式・・2つ以上の方程式を組み合わせたものを連立方程式という。
■連立方程式の解・・連立方程式のどの方程式も成り立たせるような文字の値の組を連立方程式の解といい、解を求めることを連立方程式を解くという。
(例)下記の連立方程式について上の表は、①を成り立たせるχ , yの値の組であり、このうち、②も成り立たせるものは、χ=6, y=4である。
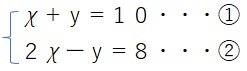
したがって、この連立方程式の解は、(χ , y)=(6, 4)










